Research - IceLab

Mathematical Modelling: Our Grand Approach

The fossil record, social networks, phytoplankton, DNA folding, microbial economics, invasive species, and antibiotic resistance. IceLab research covers a wide array of scientific questions and traverses scientific disciplines. However, all IceLab research shares a common feature: an application of mathematical modeling techniques to scientific questions. By adopting a quantitative approach, our researchers can communicate across disciplines and identify new and exciting opportunities for collaborations and discovery.

Below we discuss some broad areas of modeling techniques that unite our research, and introduce the joint theme that connects many Icelabbers: modeling adaptive mechanisms in living systems under stress.

Modeling adaptive mechanisms in living systems under stress
Eco-evolutionary Modeling
Networks
Biophysical Modeling

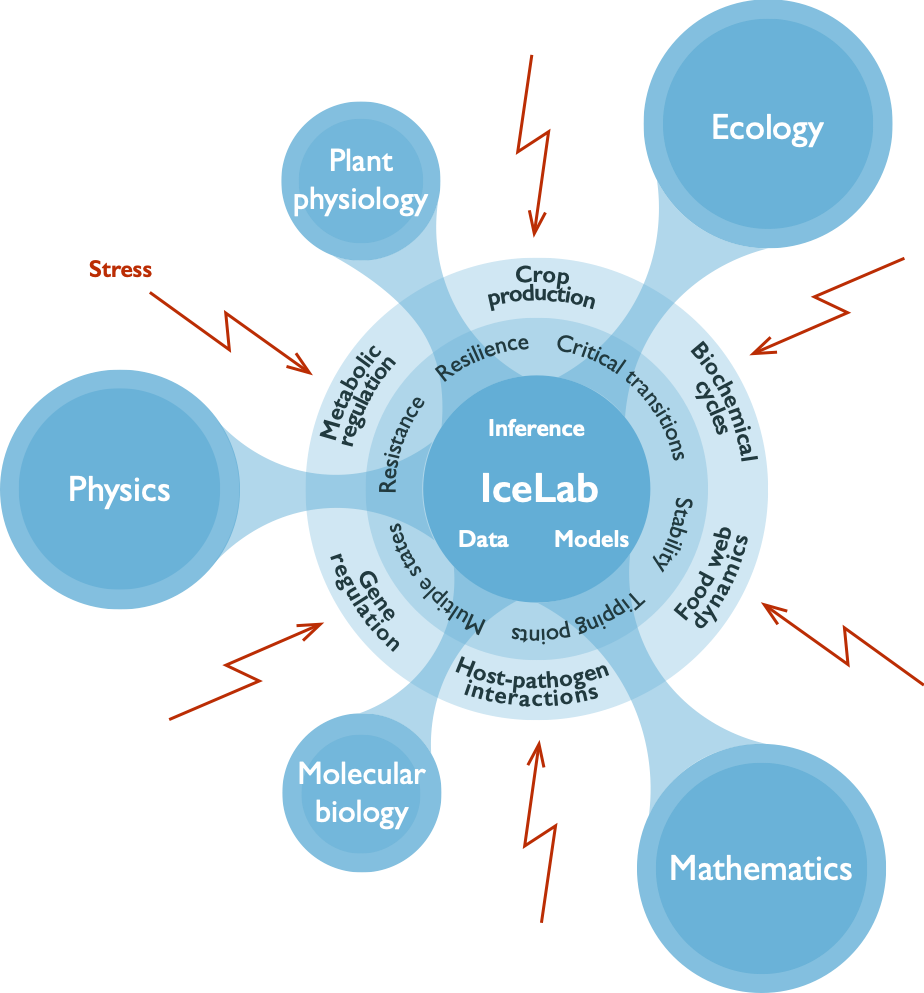
Stress Response Modeling at IceLab

Stress Response Modeling at IceLab is a multidisciplinary complexity center formed to unveil universal principles and adaptive mechanisms in living systems under stress, which explain conditions for the emergence of stability, resilience and resistance in contrast with multiple states, critical transitions and tipping points. We conduct research across three pillars: 1) system-specific empirical knowledge shared across organizational scales of study systems, 2) network analysis with new inference tools for predictions and mechanistic hypotheses, and 3) dynamical systems modeling explaining how those systems drive or inhibit critical transitions. Funded by a Swedish Research Council centre of research excellence grant, with support from Kempestiftelserna and Knut och Alice Wallenbergs Stiftelse, Stress Response Modeling at IceLab includes recruitment possibilities, a graduate research school, activities and conferences.

Stress Response Modeling at IceLab

Eco-evolutionary Modelling

With human activities drastically altering natural habitats and impacting future climatic conditions, there is an increasing need for understanding the ecology of interactions between plants, animals, and the environment, as well as how plants and animals adapt through evolutionary change. As these systems often have many complex dependencies, precise representations using the language of mathematics are often helpful to elucidate dependencies and test hypothesis. The study of ecology and evolution is also important for understanding the natural world that we are all part of.

Researchers at IceLab address questions in ecology and evolution by developing mathematical models. The models are interfaced with experimental or observational data and studied through a combination of analytical and computational methods. Although most research thus far has focused on questions in ecology and evolution, the techniques used are general and can be applied to many other areas as well, such as forestry, fisheries, social sciences and economics. The research is often done in interdisciplinary constellations with collaborators from all around the world.

As an example of ongoing projects, we are developing lake-ecosystem models as part of the larger research project “Climate change induced regime shifts in northern lake ecosystems” funded by the Knut and Alice Wallenberg Foundation. Here, the aim is to describe how biotic factors such as phytoplankton, benthic plankton, benthic grazers, and consumers at higher trophic levels interact with abiotic factors such as light availability, nutrient availability and lake morphology to determine lake productivity, biotic composition and carbon sequestration. The developed models are validated with observational data and used, among other ends, to assess the potential for regime shifts.

Networks

The whole of a complex system is the sum of its parts, plus the interactions between the parts. Understanding social, biological, and economic systems therefore often depends on understanding their patterns of interactions – their networks of nodes and links. Central questions include: How do the networks form? How do the networks guide flows across the systems? And how do the networks change over time?

In IceLab, we combine interaction data and simple models of dynamical processes on networks to identify essential nodes or substructures for different functions. Because representing interactions in complex systems with pairwise links can obscure flows across the systems, we develop higher-order representations that capture actual paths. Since networks often are big and complex in themselves, we also develop mathematics, algorithms, and visualizations to simplify and highlight important structures in standard and higher-order networks.

In our interdisciplinary approach, new models and tools allow us to study natural phenomena in new ways, which raise further questions that require refined models and tools. Ongoing projects that benefit from this tight integration of mathematical modeling and empirical sciences include decoding signaling networks controlling plant stress responses, mapping historical seasonal outbreaks for reliable modeling of the spread of disease, and delimiting bioprovinces for assessing how they respond to past and present major climatic changes.

Biophysical Modelling

Biological systems in cells provide particular challenges to researchers seeking to understand those systems through modelling. For example, biological systems often consume energy and are therefore out of equilibrium. This is the case for cellular processes like gene transcription and the fueling of biochemical reactions. We also see that systems’ dynamics often stem from networks of feedback loops that control the concentration of different types of proteins, for example in signalling and in metabolic networks, as well as in gene regulation. Additionally, cellular processes are stochastic as a result of thermal and low molecule number fluctuations.

In biophysical modelling, the Master equation is often used to handle these challenges. The Master equation is a phenomenological set of first-order differential equations that describe the time evolution of the probability for a system to be in one of a discrete set of states. Monte Carlo simulations, like the Gillespie algorithm, are also used. At IceLab, we have used these methods to study protein diffusion on a crowded DNA molecule, protein target search in the nucleus, and epigenetic repression by Polycomb proteins in fruit fly.

At IceLab, we also have projects on the 3D organisation of DNA in the nucleus. To study this, we use molecular dynamics simulations of polymer systems using free available packages, such as GROMACS, but also self-written code. In addition, we use network clustering algorithms, to better understand the network of physical contacts between DNA fragments that experimental researchers measure using so-called Hi-C experiments.

Science that speaks plainly

We believe anyone should be able to grasp the findings of any scientist’s research studies. To that end, we feature summaries of IceLab work on this page that is accessible and interesting.